We're always looking for entertaining and instructive speed problems. Unlike like the young racers above, our goal today isn't to cross the finish line first; it's to further develop our checker visualization skills, and one way to do that is with a good problem solved against the clock.

Regular contributors Josh and Lloyd Gordon of Toronto sent us a speed problem that is relatively easy, but quite surprisingly, it arose in actual over the board play. You'll see what we mean when you solve it.

Click on the link below to display the problem and start our unforgiving Javascript clock. Then come back and click on Read More to check your solution.

February 2016 Speed Problem (easy, 5 seconds)

We hope that your holiday season is going well, and that it is filled with everything you might wish for. Our holidays definitely include time for checkers, and today we'd like to turn to someone who was without doubt one of the greatest American players of his day, Samuel Gonotsky.

Mr. Gonotsky suffered from poor health made worse by his reputed lack of interest in taking care of himself, and a perennial lack of money. Had he lived beyond his twenties, who knows what checker mountains he might have climbed?

Today, let's look at one of his relatively few problem positions.

BLACK

WHITE
White to Play and Draw

W:W27,25,17,13:B19,18,12,10.

This one will require some thought, so maybe it's one to try to solve with that cup of coffee after dinner or a slice of leftover mince pie. It's up to you how to go about it, but the main thing is to enjoy. When you're ready, click on Read More to see the solution.

(Editor's Note: The next installment of The Lindyville Checker Club serial will be delayed until January 9 so that we may accommodate today's special column.)

This week the release of the seventh film in the immortal Star Wars saga is big news. Star Wars promotions and features are everywhere, and The Checker Maven is joining in with our own entry.

In checkers a star move is the only move possible in a given situation to obtain a win or a draw, as the case may be. In today's problem, Black can get a draw only by making five consecutive "star" moves. Star Wars indeed!

WHITE

BLACK
Black to Play and Draw

B:WK23,K1:BK21,9.

Black has a tough position, but the force is with him and if he navigates the "star" wars he can obtain a draw.

Is the force with you? Can you "force" a draw by solving the "star" wars? "Do. Or do not. There is no 'try'"--- Jedi Master Yoda.

When you're ready, force your mouse onto Read More to try out the solution.

We meant "CCCP" to stand for "Clever Canadian Checker Problem" since we found today's speed problem in the pages of an old edition of Canadian Checker Player. But our art department came up with a bilingual pun, and we thought it was pretty good. (Extra credit if you can explain it on your own.)

The problem really isn't so hard. But the holiday season is approaching, and we're feeling extra-generous, so we're giving you 15 seconds to solve it. When you're ready, click on the link below, then come back and click on Read More to check your solution.

December 2015 Speed Problem

This is Thanksgiving weekend, definitely our favorite time of year, when the wonderful Thanksgiving holiday is celebrated in the United States. It's a great family time, with food--- lots of it--- and festivity and reflection on the many things for which we all can be grateful.

On such occasions we like to feature a Tom Wiswell problem. Mr. Wiswell, a great checker champion, checker writer, and American patriot, represents for us the spirit of America and the spirit of the American holidays.

This year we've picked out a problem that is a real dandy.

BLACK

WHITE
White to Play and Win

W:W10,13,15,25,30,31:B1,2,6,20,K24.

White is a piece up, but Black has a king and the White win is yet to be demonstrated. It's a practical problem but not necessarily an easy one.

So, see how you can do. Take your time; it's a holiday weekend and some leisurely checker enjoyment is most appropriate. When you're done, click on Read More to see the solution. Then, do as we invite you to do every year at this time--- help yourself to another slice of pumpkin pie.

Public Domain

Josh and Lloyd Gordon of Toronto have been regular contributors to The Checker Maven, and we're most grateful for it. The Gordons spend many of those long Canadian winter nights playing checkers at home, and we've noticed that over time their checkerboard skills have been growing steadily.

So we weren't all too surprised when the Gordons sent us an interesting problem position with a very clever and very pleasing solution. Better still, the position arose in the course of over the board play.

The initial position was this.

BLACK

WHITE
White to Play
W:W31,30,28,27,26,25,23,21,19,18,15,13:B24,20,14,12,11,10,9,8,6,5,3,2.

The next few moves are pretty clear: 25-22 (there's nothing else) 22-17 (likewise) 22-17 (certainly not 19-16) 11-16 which now gives us the situation diagrammed below.

BLACK

WHITE
White to Play and Draw
W:W31,30,28,27,26,23,21,19,18,17,15,13:B24,20,16,14,12,10,9,8,7,6,5,3.

Things really don't look so great for White, yet there's a star move that draws, although both sides will have to play quite carefully until the position is settled.

This is not an easy problem by any means, but it's a great challenge, whether or not many months of long, cold winter nights lay ahead for you. Don't freeze up; give it your best, then thaw out the solution by clicking on Read More.

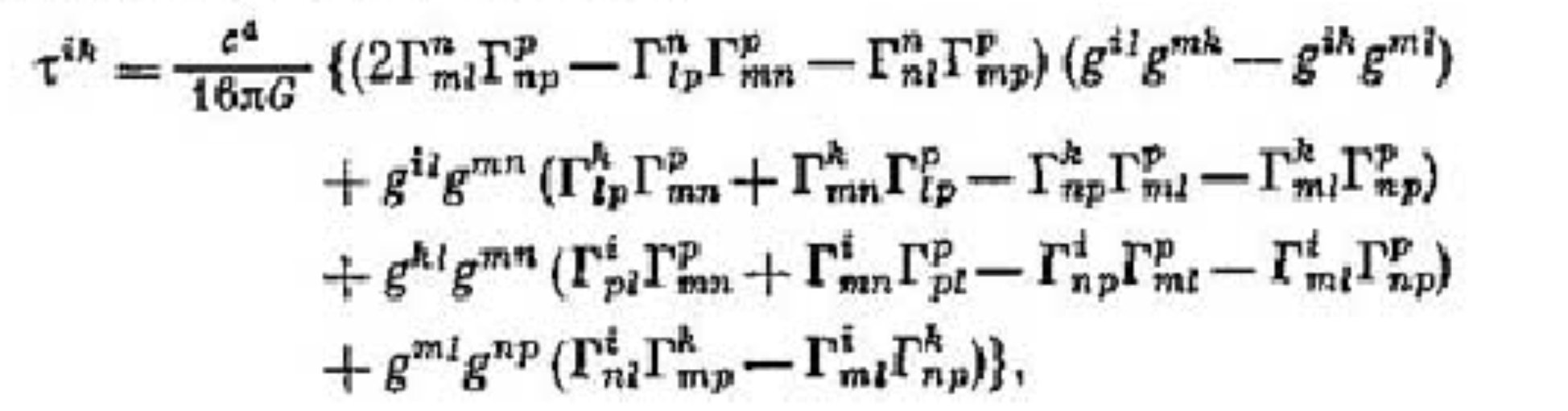
"Advanced" problems are an interesting thing. They're supposed to be difficult, usually targeting an expert practitioner in search of a real challenge. But, properly explained, such problems can be of great use to us lesser mortals, too. Today's problem, we think, is an example of that.

It's definitely a Black win, but is this an "advanced" problem? We'd rank it perhaps as "advanced intermediate" rather than "expert." What do you think? The real point, though, is that the solution demonstrates a winning technique that is useful and practical.

When you've advanced your knowledge by solving the problem, advance your mouse to Read More to see the solution and explanatory notes.

We haven't had a regular speed problem in a little while, so today we're returning to that theme and subjecting you once again to our unforgiving Javascript clock. The good news, though, is that the problem is very easy.

Oh .. the bad news? You'll have five seconds to solve it!

Fear not. Most players will see it at a glance, but if it takes you a little longer, no matter. Working it out is what really counts.

When you're ready, click on the link below. After you've solved it come back and click on Read More to verify your solution.

August Speed Problem (very easy, 5 seconds)

Each year we mark Labor Day, the celebration of the men and women who make America what it is --- the workers of our nation. From factory worker to small business owner, from taxi driver to doctor, millions of Americans keep our nation going and help make it strong. We're not ones to make class distinctions; we believe that all honest work is worthy of respect and recognition.

The sketch above is of one of the very first Labor Day celebrations, in New York City way back in 1882.

Often on great American holidays we turn to Tom Wiswell, but today we instead offer a setting by another great American problemist of days gone by, Charles Hefter. Mr. Hefter's settings meet Mr. Wiswell's criteria of being natural, clever, and pleasing. Here's one that's simple in form and challenging in execution.

WHITE

BLACK
Black to Play and Win

B:W23,21,19,13:B14,6,3,1.

The position is from a game played about 80 years ago; in the actual event, the game was drawn. Mr. Hefter later showed that Black has a win. Can you find it? Labor away and when your work is done, click on Read More to see the solution and notes.

In the chart above, Apple Computer has the "nice problem" of having to figure out what to do with all the money they've made.

"A nice problem to have" is a phrase often heard when someone faces a "dilemma" in which any choice is a good one. Here in Hawai`i, we sometimes have to decide between going to the beach or going to the mall. That's considered a nice problem to have, especially in January.

"A nice problem" in checkers of course means something else, and this week's position, attributed to W. J. Wood, is an example. Mr. Wood himself, after presenting the run-up, stated "Now we have a nice problem." Did he intend a pun or play on words? We rather doubt it.

WHITE

BLACK
Black to Play and win

B:W29,21,20,K6:B16,K14,11,9,7.

We'll warn you that the solution is very long, but it is also very methodical, and you should be able to work out the general direction if not every detail. There is a trap or two along the way, however, so be careful, and when you've given it a nice try, click your mouse nicely on Read More to see the solution and notes.