The Checker Maven
The World's Most Widely Read Checkers and Draughts Publication
Bob Newell, Editor-in-Chief
Published every Saturday morning in Honolulu, Hawai`i
Noticing missing images? An explanation is here.
As Easy As Pie

Public Domain
We've often said that we present a range of problems in our Checker Maven columns; sometimes they're grandmaster tough, sometimes beginner easy, but most are usually somewhere in-between. We have readers with a very wide range of skills, and we try to provide something for everyone. We suggest the following: when you find a problem is tough, study the solution with a view to learning technique; when it seems easy, try for rapid sight recognition.
Today, though, we've got a truly easy-as-pie problem that even many early-stage checkerists will solve right away. See how quickly you can spot the solution!

BLACK
Black to Play and Win
B:W15,12,K9:B7,3,K1.
By the time you read this line, you've probably already solved it, but just in case, you can ease over to Read More to check your answer.![]()
Winter Break

If you live in a cold North American climate, you probably can use a bit of a winter break. Now, there's a definite difference between a winter break--- an escape from the cold--- and a spring break, which is often associated with hijinx on the part of college students.
But we think a winter break can also stand a bit of mischief, at least of the checker nature. So we've chosen a problem that was originally titled "Maryland Mischief." Surely, Maryland can suffer from some serious winter weather, and perhaps this is a Marylander's way of taking a break. Have a look and see what you think.

WHITE
White to Play, What Result?
W:B7,11,17,22,24,K18,K31:W8,19,28,29,K4,K25.
Attributed to a Wilson Coudon of Elkton, Maryland, you can tell you're in for some mischief from the problem terms alone, as it's one of those "What Result?" puzzlers that often leave you guessing. That diagonal lineup looks pretty mischievious, too. Perhaps the fact that White is down a piece will provide a clue?
Take a short winter break and see what you can do with this one, then click your playful mouse on Read More to see the solution.![]()
Le rouge et le noir

Levavasseur, libraire, Palais-Royal, 1831., CC BY-SA 4.0
We've received a comment from a highly respected reader to the effect that our speed problems are confusing and as a result, unfair. Our reader has asked us to state in advance the terms of the problem and to allow a little extra "orientation" time. Not displaying the Javascript clock was another suggestion, as the reader deemed it distracting.
We're trying out some of these ideas today. By eliminating the clock, of course, we eliminate the timed challenge and in a way negate the idea of a "speed" problem; the idea will be to simply see how fast you can spot the solution, without any external pressure.
The reader also suggested that since our diagrams show Red and White pieces, we should discontinue use of the term "Black" in favor of "Red." That's a bit more complicated, in that much of the literature we quote uses the terms "Black" and "White." In our early days, we indeed used black and white diagrams, but the red and white proved much more popular.
What to do? Red or Black? Le rouge ou le noir? For now, we're continuing with Black rather than Red, but we'd love to hear your opinions. Write to us at redorblack@checkermaven.com.
But let's go ahead and look a typical speed problem. Black (Red) is at the bottom of the board, moving up, and the terms are Black (Red) to play and win. There's no clock and so no particular time limit. We've also provided both a Red/White and a Black/White diagram. Which do you prefer?

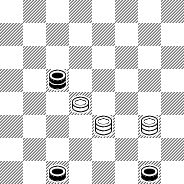
BLACK
Black to Play and Win
B:W15,K10,K9:BK19,3,1.
BLACK
Black to Play and Win
B:W15,K10,K9:BK19,3,1.
Click on Read More when you're ready to check your solution.![]()
Easy Peasy

We were surprised to learn that the expression "easy peasy" is relatively modern, having first made its appearance around 1976, apparently as part of an advertisement for dishwashing liquid that went "easy peasy, lemon squeezy." The expression has since come to mean, of course, something simple or easy.
Today's problem falls in that category. The Checker Maven tries to present a range of problems, from beginner through grandmaster level, and we know that an easy one is often a quick and welcome diversion.
So, here's today's "easy peasy" position.

WHITE
White to Play and Win
W:W32,27,26,25,22,21,11:B19,18,15,12,4,2,1.
You won't have much trouble with this one, and the solution is rather nice, although there are a couple of ways to go wrong. When you're ready, an easy peasy click on Read More will reveal everything.![]()
January Kickoff

Did you watch football on New Year's Day? Although we're writing this column weeks in advance, we can tell you for sure that no, The Checker Maven staff didn't watch football on New Year's Day or any other day, although we do admit to having seen a football game on television as recently as 1978. We understand football's great popularity, but it just isn't our thing.
So instead we'll kick off our checker year with a game that dates back even further, to 1908. The game is a bit flawed but nonetheless an interesting over the board contest. Let's have a look.
| 1. | 10-15 | 23-18 |
| 2. | 12-16 | 26-23 |
| 3. | 16-20 | 21-17 |
| 4. | 9-13 | 17-14 |
| 5. | 8-12 | 14-9 |
| 6. | 5x14 | 18x9 |
| 7. | 4-8 |
7-10 was likely better here, though the text move certainly allows for a draw.
| 7. | ... | 24-19 |
| 8. | 15x24 | 28x19 |
| 9. | 7-10 |
11-15 evaluates to a likely draw and may be best. Deep analysis also evaluates the current position as a probable draw that may be more difficult to find over the board.
| 9. | ... | 23-18 |
22-18 was correct. The edge passes to Black who now might win.
| 10. | 11-16 | 27-23 |
| 11. | 20-24 | |
This unfortunate move turns a probable Black win into a certain White win, and now your New Year's task is twofold. First, correct this last error and give what could have been Black's winning move. Then, continuing on from the text move, show how White wins (it's rather easy). When you've got it, click on Read More to see the solution.

WHITE
White to Play and Win
W:W32,31,30,29,25,23,22,19,18,9:B24,16,13,12,10,8,6,3,2,1.
![]()
New Year's Eve 2016

Are you thinking checkers or partying today? We realize that this column will appear on New Year's Eve, and you may not have a lot of time for checkers today (sad as that might be). So we'll give you something quite a bit easier than usual this week, and we won't even annoy you with our Javascript clock.

WHITE
White to Play and Win
W:W26,19,16,15,11:BK30,K24,14,12.
Easier? Did we say easier? Actually, it is, and it won't take time away from your celebrations. So work it out, check your solution by clicking on Read More, and then have a happy and safe New Year's Eve.
Happy New Year from The Checker Maven!![]()
Happy Holidays 2016

The Checker Maven wishes all of our readers the happiest of holiday seasons. Regardless what holiday you might celebrate or how you might celebrate it, we hope this time of year brings you happiness and contentment.
During the holidays perhaps you have a little more free time, but even if you're busier than can be, one can always make time for some checkers. Today we present a study by that renowned player and author, the late Ken Grover; it's quite interesting and should give you plenty of holiday checker enjoyment.

WHITE
White to Play and Win
W:W30,28,27,26,22,21,20,18:B16,15,13,11,10,9,7,5.
Can you find a winning line of play? We'll be fair about it: Mr. Grover published one win and the computer found another that was similar but not quite the same. See if you can work it out and then click on Read More to see the solutions.![]()
Coffee and Cake, 2016

A bit of a holiday season tradition at The Checker Maven has been the presentation of a "coffee and cake" problem. This is the sort of problem that you show to your checker friends and bet them coffee and cake that they can't solve it.
We think this year we have one that will put you in the winner's circle and garner you a nice Saturday afternoon treat at your local café or coffee shop. Let's have a look.

WHITE
White to Play and Draw
W:W16,14,12,11:B13,6,5,4.
You might initially ask, what's the difficulty? Are those Checker Maven people asking me to just give away some coffee and cake? But when you take a closer look, you'll see that White is mighty short of options. Maybe your friends won't get their coffee and cake so easily after all.
Now, it's only fair for you to try to solve this one first, before you spring it on your unsuspecting friends, don't you agree? So give it your all, and then click on Read More to see the solution.![]()
12 Years

Today The Checker Maven completes a dozen years of no-fail weekly publication, something we modestly believe is a significant accomplishment. We hope we've being doing our share in promoting the great game of checkers, and we do hope to be able to continue publishing for at least a few more years.
Someone who has contributed immensely to our game is Richard Pask, and to celebrate the "12" theme, we're taking a position that arises from Ballot 12 in his upcoming book, Complete Checkers. (It will be published by us most likely in spring 2017.)

WHITE
White to Play and Win
W:W12,19,20,24,29,30,31,32:B3,4,6,8,9,11,13,17.
Black has just blundered with 2-6 instead of the "star" move given in the Complete Checkers text, 17-22. How does White bring home the win? We suppose you ought to get 12 minutes to solve it, or 12 attempts, or something of the sort, but just do the best you can. Then, you can click on Read More once (not 12 times) to see the solution.![]()
Thanksgiving Weekend 2016

We've always written about how we love the Thanksgiving holiday, a holiday that unites everyone. No matter what your race, religion, color, or political leanings, giving thanks is an American tradition that we can all support.
On this wonderful weekend we usually try to feature a problem from a great American composer or great American players. Today we'll look at a position that arose in a match game between two of the all-time greats, Walter Hellman and Maurice Chamblee.

BLACK
Black to Play and Win
B:W31,30,28,27,22,21,15:B19,16,13,9,8,7,5,3.
Black is a piece up, and you'd think he should win handily. But it isn't as easy as all that. Can you find the right line of play that will carry Black to victory? You may be surprised!
Find the way to the laurel wreath, and then click on Read More to see the solution.![]()
The Checker Maven is produced at editorial offices in Honolulu, Hawai`i, as a completely non-commercial public service from which no income is obtained or sought. Original material is Copyright © 2004-2025 Avi Gobbler Publishing. Other material is public domain, AI generated, as attributed, or licensed under CC1, CC2,CC3 or CC4. Information presented on this site is offered as-is, at no cost, and bears no express or implied warranty as to accuracy or usability. You agree that you use such information entirely at your own risk. No liabilities of any kind under any legal theory whatsoever are accepted. The Checker Maven is dedicated to the memory of Mr. Bob Newell, Sr.

